《安徽省長豐縣高中數(shù)學(xué) 第三章 導(dǎo)數(shù)及其應(yīng)用 3.2 導(dǎo)數(shù)的計(jì)算 3.2.2 基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則教案 新人教A版選修11》由會(huì)員分享���,可在線閱讀���,更多相關(guān)《安徽省長豐縣高中數(shù)學(xué) 第三章 導(dǎo)數(shù)及其應(yīng)用 3.2 導(dǎo)數(shù)的計(jì)算 3.2.2 基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則教案 新人教A版選修11(7頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索���。
1���、
3.2.2基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則
項(xiàng)目
內(nèi)容
課題
(共 1 課時(shí))
修改與創(chuàng)新
教學(xué)
目標(biāo)
1.熟練掌握基本初等函數(shù)的導(dǎo)數(shù)公式���;
2.掌握導(dǎo)數(shù)的四則運(yùn)算法則;
3.能利用給出的基本初等函數(shù)的導(dǎo)數(shù)公式和導(dǎo)數(shù)的四則運(yùn)算法則求簡單函數(shù)的導(dǎo)數(shù).
教學(xué)重���、
難點(diǎn)
教學(xué)重點(diǎn):基本初等函數(shù)的導(dǎo)數(shù)公式���、導(dǎo)數(shù)的四則運(yùn)算法則
教學(xué)難點(diǎn): 基本初等函數(shù)的導(dǎo)數(shù)公式和導(dǎo)數(shù)的四則運(yùn)算法則的應(yīng)用
教學(xué)
準(zhǔn)備
多媒體課件
教學(xué)過程
一、導(dǎo)入新課:
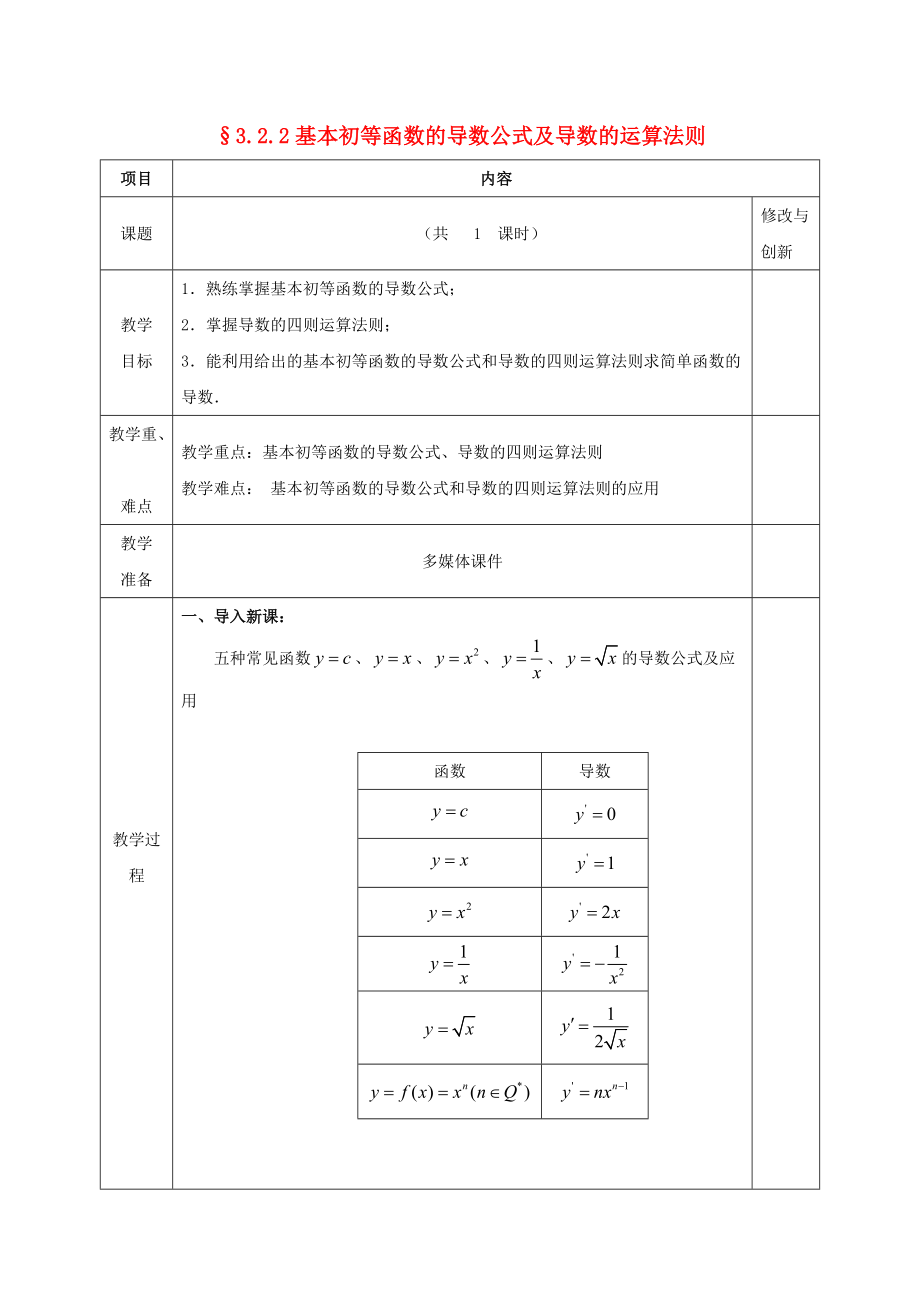
五種常見函數(shù)���、���、、���、的導(dǎo)數(shù)公式及應(yīng)用
函數(shù)
導(dǎo)數(shù)
2���、
二、講授新課:
(一)基本初等函數(shù)的導(dǎo)數(shù)公式表
函數(shù)
導(dǎo)數(shù)
(二)導(dǎo)數(shù)的運(yùn)算法則
導(dǎo)數(shù)運(yùn)算法則
1.
2.
3.
(2)推論:
(常數(shù)與函數(shù)的積的導(dǎo)數(shù)���,等于常數(shù)乘函數(shù)的導(dǎo)數(shù))
三.典例分析
例1.假設(shè)某國家在20年期間的年均通貨膨脹率為���,物價(jià)(單位:元)與時(shí)間(單位:年)有如下函數(shù)關(guān)系���,其中為時(shí)的物價(jià).假定某種商品的,那么在第10個(gè)年頭���,這種商品的價(jià)格上漲的速度大約是多少(精確到0.01)���?
解:根據(jù)
3、基本初等函數(shù)導(dǎo)數(shù)公式表���,有
所以(元/年)
因此���,在第10個(gè)年頭,這種商品的價(jià)格約為0.08元/年的速度上漲.
例2.根據(jù)基本初等函數(shù)的導(dǎo)數(shù)公式和導(dǎo)數(shù)運(yùn)算法則���,求下列函數(shù)的導(dǎo)數(shù).
(1) (2)���;
(3); (4)���;
(5).(6);(7)
解:(1)���,
���。
(2)
(3)
(4)���,
。
(5)
(6)
���,
���。
(7)
。
【點(diǎn)評】
① 求導(dǎo)數(shù)是在定義域內(nèi)實(shí)行的.
② 求較復(fù)雜的函數(shù)積���、商的導(dǎo)數(shù)���,必須細(xì)心、耐心.
例3日常生活中的飲水通常是經(jīng)過凈化的.隨著水純凈度的提高���,所需凈化費(fèi)用不斷增加
4���、.已知將1噸水凈化到純凈度為時(shí)所需費(fèi)用(單位:元)為
求凈化到下列純凈度時(shí),所需凈化費(fèi)用的瞬時(shí)變化率:(1) (2)
解:凈化費(fèi)用的瞬時(shí)變化率就是凈化費(fèi)用函數(shù)的導(dǎo)數(shù).
(1) 因?yàn)椋?��,純凈度為時(shí)���,費(fèi)用的瞬時(shí)變化率是52.84元/噸.
(2) 因?yàn)椋?��,純凈度為時(shí)���,費(fèi)用的瞬時(shí)變化率是1321元/噸.
函數(shù)在某點(diǎn)處導(dǎo)數(shù)的大小表示函數(shù)在此點(diǎn)附近變化的快慢.由上述計(jì)算可知,.它表示純凈度為左右時(shí)凈化費(fèi)用的瞬時(shí)變化率���,大約是純凈度為左右時(shí)凈化費(fèi)用的瞬時(shí)變化率的25倍.這說明���,水的純凈度越高,需要的凈化費(fèi)用就越多���,而且凈化費(fèi)用增加的速度也越快.
四.課堂練習(xí)
1.課
5���、本P92練習(xí)
2.已知曲線C:y =3 x 4-2 x3-9 x2+4,求曲線C上橫坐標(biāo)為1的點(diǎn)的切線方程���;
(y =-12 x +8)
課堂小結(jié):
(1)基本初等函數(shù)的導(dǎo)數(shù)公式表
(2)導(dǎo)數(shù)的運(yùn)算法則
布置作業(yè):P85. 4,5,6
板書設(shè)計(jì)
3.2.2基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則
(一)基本初等函數(shù)的導(dǎo)數(shù)公式表
函數(shù)
導(dǎo)數(shù)
(二)導(dǎo)數(shù)的運(yùn)算法則
導(dǎo)數(shù)運(yùn)算法則
1.
2.
3.
例1���、例2、例3
教學(xué)反思
基本
6���、初等函數(shù)的導(dǎo)數(shù)公式和導(dǎo)數(shù)的運(yùn)算法則只給出結(jié)論���,不要求學(xué)生把握它們的推導(dǎo)過程。這些公式要求學(xué)生能熟練記憶���,并會(huì)應(yīng)用它們進(jìn)行求導(dǎo)���。求較復(fù)雜的函數(shù)積、商的導(dǎo)數(shù)���,必須要細(xì)心���、耐心。
用具體實(shí)例���,讓學(xué)生體會(huì)學(xué)習(xí)這一內(nèi)容的意義���,并會(huì)解決相關(guān)的其他實(shí)際問題���,提高學(xué)生學(xué)習(xí)的興趣和積極性。
6EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F3756EDBC3191F2351DD815FF33D4435F375
 安徽省長豐縣高中數(shù)學(xué) 第三章 導(dǎo)數(shù)及其應(yīng)用 3.2 導(dǎo)數(shù)的計(jì)算 3.2.2 基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則教案 新人教A版選修11
安徽省長豐縣高中數(shù)學(xué) 第三章 導(dǎo)數(shù)及其應(yīng)用 3.2 導(dǎo)數(shù)的計(jì)算 3.2.2 基本初等函數(shù)的導(dǎo)數(shù)公式及導(dǎo)數(shù)的運(yùn)算法則教案 新人教A版選修11