《2013年全國高考數(shù)學第二輪復習 專題升級訓練15 概率與統(tǒng)計 文》由會員分享�,可在線閱讀�,更多相關《2013年全國高考數(shù)學第二輪復習 專題升級訓練15 概率與統(tǒng)計 文(5頁珍藏版)》請在裝配圖網(wǎng)上搜索����。
1、專題升級訓練15 概率與統(tǒng)計
(時間:60分鐘 滿分:100分)
一��、選擇題(本大題共6小題���,每小題6分��,共36分)
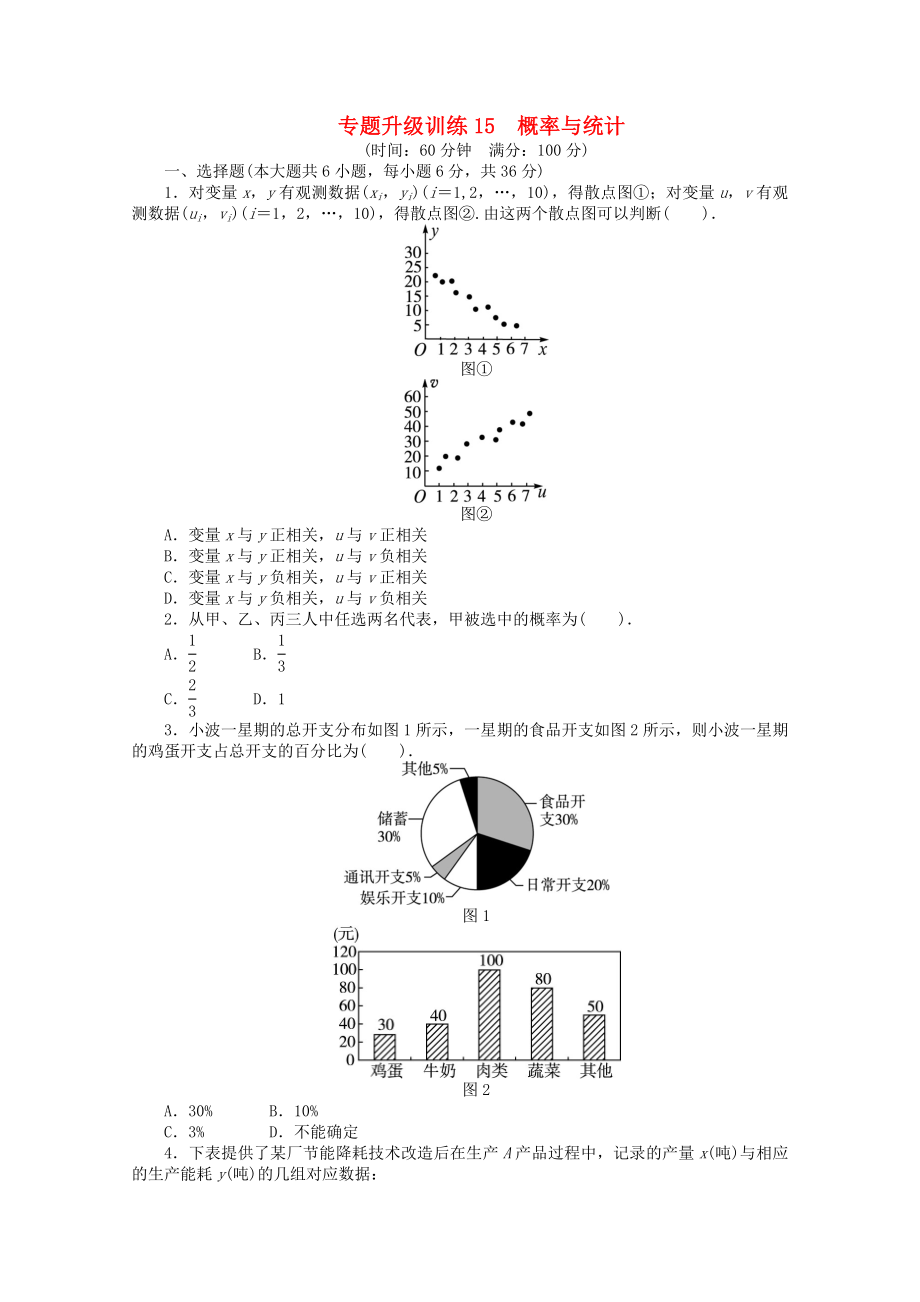
1.對變量x��,y有觀測數(shù)據(jù)(xi�����,yi)(i=1,2����,…���,10)��,得散點圖①����;對變量u���,v有觀測數(shù)據(jù)(ui��,vi)(i=1�,2�,…,10)��,得散點圖②.由這兩個散點圖可以判斷( ).
圖①
圖②
A.變量x與y正相關��,u與v正相關
B.變量x與y正相關����,u與v負相關
C.變量x與y負相關,u與v正相關
D.變量x與y負相關�,u與v負相關
2.從甲、乙�����、丙三人中任選兩名代表,甲被選中的概率為( ).
A. B.
C. D
2����、.1
3.小波一星期的總開支分布如圖1所示,一星期的食品開支如圖2所示�,則小波一星期的雞蛋開支占總開支的百分比為( ).
圖1
圖2
A.30% B.10%
C.3% D.不能確定
4.下表提供了某廠節(jié)能降耗技術改造后在生產(chǎn)A產(chǎn)品過程中,記錄的產(chǎn)量x(噸)與相應的生產(chǎn)能耗y(噸)的幾組對應數(shù)據(jù):
x
3
4
5
6
y
2.5
t
4
4.5
根據(jù)上表提供的數(shù)據(jù)�,求出y關于x的線性回歸方程為=0.7x+0.35,那么表中t的值為( ).
A.3 B.3.15
C.3.5 D.4.5
5.已知
3��、直線y=x+b�,b∈[-2,3],則直線在y軸上的截距大于1的概率是( ).
A. B.
C. D.
6.甲�����、乙兩名運動員在某項測試中的6次成績?nèi)缜o葉圖所示����,x1,x2分別表示甲�����、乙兩名運動員這項測試成績的平均數(shù)��,s1,s2分別表示甲�、乙兩名運動員這項測試成績的標準差,則有( ).
A.1>2�,s1<s2
B.1=2���,s1<s2
C.1=2�,s1=s2
D.1<2���,s1>s2
二�、填空題(本大題共3小題����,每小題6分,共18分)
7.一支田徑運動隊有男運動員56人���,女運動員42人.現(xiàn)用分層抽樣的方法抽取若干人����,若抽取的男運動員有8人�,則抽取的女運
4、動員有__________人.
8.如圖所示是某公司(共有員工300人)2012年員工年薪情況的頻率分布直方圖.由此可知�,員工中年薪在14萬~16萬元之間的共有__________人.
9.由正整數(shù)組成的一組數(shù)據(jù)x1,x2,x3��,x4��,其平均數(shù)和中位數(shù)都是2���,且標準差等于1����,則這組數(shù)據(jù)為__________.(從小到大排列)
三���、解答題(本大題共3小題����,共46分.解答應寫出必要的文字說明�、證明過程或演算步驟)
10.(本小題滿分15分)某校100名學生期中考試語文成績的頻率分布直方圖如圖所示,其中成績分組區(qū)間是:[50,60)����,[60,70),[70,80)����,[80,90)�,[90
5�、,100].
(1)求圖中a的值;
(2)根據(jù)頻率分布直方圖����,估計這100名學生語文成績的平均數(shù);
(3)若這100名學生語文成績某些分數(shù)段的人數(shù)(x)與數(shù)學成績相應分數(shù)段的人數(shù)(y)之比如下表所示�,求數(shù)學成績在[50,90)之外的人數(shù).
分數(shù)段
[50,60)
[60,70)
[70,80)
[80,90)
x∶y
1∶1
2∶1
3∶4
4∶5
11.(本小題滿分15分)為加強中學生實踐�、創(chuàng)新能力和團隊精神的培養(yǎng),促進教育教學改革����,鄭州市教育局舉辦了全市中學生創(chuàng)新知識競賽.某校舉行選拔賽,共有200名學生參加��,為了解成績情況����,從中抽取50名學生的成績(得分均
6、為整數(shù)�����,滿分為100分)進行統(tǒng)計.請你根據(jù)尚未完成的頻率分布表�,解答下列問題:
分組
頻數(shù)
頻率
一
60.5~70.5
a
0.26
二
70.5~80.5
15
c
三
80.5~90.5
18
0.36
四
90.5~100.5
b
d
合計
50
e
(1)若用系統(tǒng)抽樣的方法抽取50個樣本�,現(xiàn)將所有學生隨機地編號為000,001,002�,…,199�,試寫出第二組第一位學生的編號;
(2)求出a���,b�,c���,d�,e的值(直接寫出結果)��,并作出頻率分布直方圖���;
(3)若成績在85.5~95.5分的學生為二等獎�����,問參賽學生中獲得二等獎的學生約為多
7�、少人���?
12.(本小題滿分16分)某花店每天以每枝5元的價格從農(nóng)場購進若干枝玫瑰花��,然后以每枝10元的價格出售.如果當天賣不完���,剩下的玫瑰花做垃圾處理.
(1)若花店一天購進17枝玫瑰花���,求當天的利潤y(單位:元)關于當天需求量n(單位:枝,n∈N)的函數(shù)解析式�;
(2)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
日需
求量n
14
15
16
17
18
19
20
頻數(shù)
10
20
16
16
15
13
10
①假設花店在這100天內(nèi)每天購進17枝玫瑰花�,求這100天的日利潤(單位:元)的平均數(shù);
②若花店一天購進17枝玫瑰花
8���、,以100天記錄的各需求量的頻率作為各需求量發(fā)生的概率��,求當天的利潤不少于75元的概率.
參考答案
一���、選擇題
1.C 解析:圖①的散點分布在斜率小于0的直線附近����,y隨x的增大而減小����,故變量x與y負相關.
圖②的散點分布在斜率大于0的直線附近����,u隨v的增大而增大�,故變量u與v正相關,選C.
2.C 解析:從甲�、乙、丙三人中任選兩名代表的選法共有(甲���、乙)�����,(甲�����、丙)�����,(乙��、丙)3種�,甲被選中包含基本事件(甲���、乙)����,(甲、丙)2種��,所以甲被選中的概率為�����,故選C.
3.C 解析:由題圖2知��,小波一星期的食品開支為300元���,其中雞蛋開支為30元��,占食品開支的10%,而食品開支占總開支
9����、的30%����,所以小波一星期的雞蛋開支占總開支的百分比為3%����,故選C.
4.A 解析:由題意知,==����,=,又因為線性回歸直線=0.7x+0.35恒過(��,)點���,可得t=3�,故選A.
5.D 解析:直線y=x+b在y軸上的截距b>1����,
又b∈[-2,3],則1<b<3�����,
所以P==.
6.B 解析:依題意��,得1=(9+14+15×2+16+21)=15��,2=(8+13+15×2+17+22)=15,1=2���;s=[(9-15)2+(14-15)2+2×(15-15)2+(16-15)2+(21-15)2]≈12.3�,s=[(8-15)2+(13-15)2+2×(15-15)2+(17-15)2
10���、+(22-15)2]≈17.7��,s<s�,即s1<s2����,所以選B.
二、填空題
7.6 解析:設抽取的女運動員的人數(shù)為a����,則根據(jù)分層抽樣的特性,有=��,解得a=6.故抽取的女運動員有6人.
8.72 解析:由所給圖形可知���,員工中年薪在14萬~16萬元之間的頻率為1-(0.02+0.08+0.08+0.10+0.10)×2=0.24,所以員工中年薪在14萬~16萬元之間的共有300×0.24=72(人).
9.1,1,3,3 解析:不妨設x1≤x2≤x3≤x4�,x1,x2,x3��,x4∈N*��,依題意得x1+x2+x3+x4=8�,
s==1,
即(x1-2)2+(x2-2)2+(x3-2)2
11�、+(x4-2)2=4,所以x4≤3.
則只能是x1=x2=1�����,x3=x4=3�,則這組數(shù)據(jù)為1,1,3,3.
三、解答題,
10.解:(1)依題意得�,10×(2a+0.02+0.03+0.04)=1,解得a=0.005.
(2)這100名學生語文成績的平均數(shù)為:55×0.05+65×0.4+75×0.3+85×0.2+95×0.05=73.
(3)數(shù)學成績在[50,60)的人數(shù)為:100×0.05=5��,
數(shù)學成績在[60,70)的人數(shù)為:100×0.4×=20��,
數(shù)學成績在[70,80)的人數(shù)為:100×0.3×=40��,
數(shù)學成績在[80,90)的人數(shù)為:100×0.2×=25��,
12�、
所以數(shù)學成績在[50,90)之外的人數(shù)為:100-5-20-40-25=10.
11.解:(1)編號為004.
(2)a,b,c����,d,e的值分別為13,4,0.30,0.08,1.
頻率分布直方圖如圖:
(3)在被抽到的學生中獲二等獎的人數(shù)為9+2=11(人)��,
占樣本的比例是=0.22�,即獲二等獎的概率為22%,所以獲二等獎的人數(shù)估計為200×22%=44(人).
答:獲二等獎的大約有44人.
12.解:(1)當日需求量n≥17時����,利潤y=85.
當日需求量n<17時,利潤y=10n-85.
所以y關于n的函數(shù)解析式為
y=(n∈N).
(2)①這100天中有10天的日利潤為55元��,20天的日利潤為65元���,16天的日利潤為75元�,54天的日利潤為85元����,所以這100天的日利潤的平均數(shù)為
(55×10+65×20+75×16+85×54)=76.4(元).
②利潤不低于75元當且僅當日需求量不少于16枝.故當天的利潤不少于75元的概率為
P=0.16+0.16+0.15+0.13+0.1=0.7.
 2013年全國高考數(shù)學第二輪復習 專題升級訓練15 概率與統(tǒng)計 文
2013年全國高考數(shù)學第二輪復習 專題升級訓練15 概率與統(tǒng)計 文