《高三數(shù)學(xué) 第31課時(shí) 三角函數(shù)的圖像和性質(zhì)(2)教案》由會(huì)員分享�,可在線閱讀�����,更多相關(guān)《高三數(shù)學(xué) 第31課時(shí) 三角函數(shù)的圖像和性質(zhì)(2)教案(4頁(yè)珍藏版)》請(qǐng)?jiān)谘b配圖網(wǎng)上搜索。
1���、課題:三角函數(shù)的圖象和性質(zhì)(二)
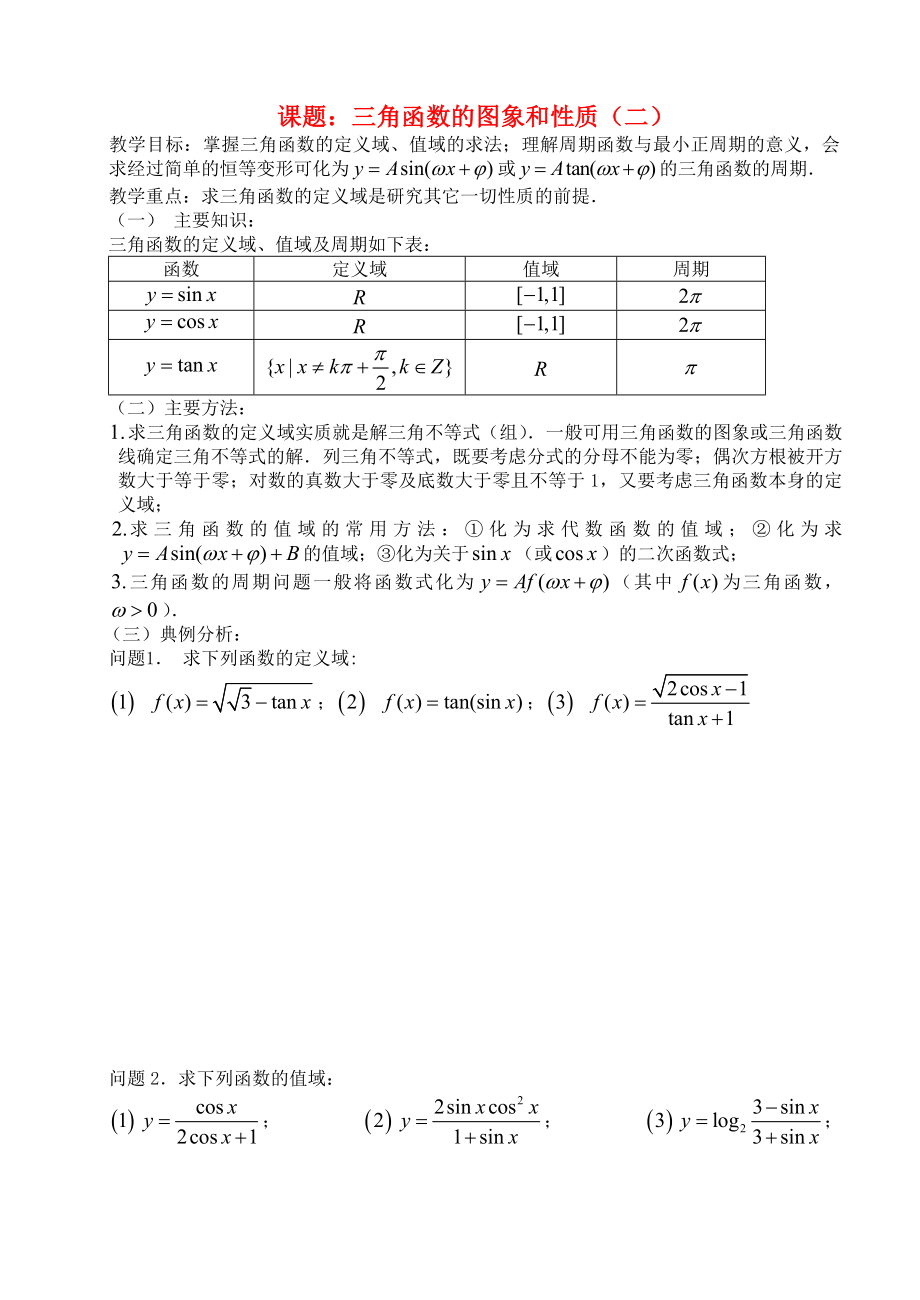
教學(xué)目標(biāo):掌握三角函數(shù)的定義域��、值域的求法;理解周期函數(shù)與最小正周期的意義�����,會(huì)求經(jīng)過(guò)簡(jiǎn)單的恒等變形可化為或的三角函數(shù)的周期.
教學(xué)重點(diǎn):求三角函數(shù)的定義域是研究其它一切性質(zhì)的前提.
(一) 主要知識(shí):
三角函數(shù)的定義域、值域及周期如下表:
函數(shù)
定義域
值域
周期
(二)主要方法:
求三角函數(shù)的定義域?qū)嵸|(zhì)就是解三角不等式(組).一般可用三角函數(shù)的圖象或三角函數(shù)線確定三角不等式的解.列三角不等式��,既要考慮分式的分母不能為零�;偶次方根被開(kāi)方數(shù)大于等于零���;對(duì)數(shù)的真數(shù)大于零及底數(shù)大于零且不等于1���,又
2、要考慮三角函數(shù)本身的定義域�����;
求三角函數(shù)的值域的常用方法:①化為求代數(shù)函數(shù)的值域��;②化為求的值域���;③化為關(guān)于(或)的二次函數(shù)式�;
三角函數(shù)的周期問(wèn)題一般將函數(shù)式化為(其中為三角函數(shù)�����,).
(三)典例分析:
問(wèn)題1. 求下列函數(shù)的定義域:
; �����;
問(wèn)題2.求下列函數(shù)的值域:
�����;�;;.
問(wèn)題3.求下列函數(shù)的周期:
�;����;
問(wèn)題4.已知函數(shù)的定義域?yàn)椋涤驗(yàn)?�,求常?shù)的值.
(四)課
3���、后作業(yè):
求函數(shù)的定義域.
函數(shù)的定義域?yàn)?
若方程有解�,則
(江西)設(shè)函數(shù),則為
周期函數(shù)��,最小正周期為 周期函數(shù)����,最小正周期為
周期函數(shù)����,數(shù)小正周期為 非周期函數(shù)
(全國(guó)Ⅱ)函數(shù)的最小正周期是 2
函數(shù)的最小正周期為
函數(shù)的周期是
已知函數(shù)���,求的定義域,判斷它的奇偶性��,并求其值域
(五)走向高考:
(四川)函數(shù)的最小正周期為
(上海)函數(shù)的最小正周期
(福建)已知函數(shù)在區(qū)間上的最小值是�,則
的最小值等于
(安徽文)解不等式.
(天津)已知函數(shù)���,.
(Ⅰ)求函數(shù)的最小正周期����;
(Ⅱ)求函數(shù)在區(qū)間上的最小值和最大值.
(重慶)設(shè).(Ⅰ)求的最大值及最小正周期;
(Ⅱ)若銳角滿足����,求的值.
 高三數(shù)學(xué) 第31課時(shí) 三角函數(shù)的圖像和性質(zhì)(2)教案
高三數(shù)學(xué) 第31課時(shí) 三角函數(shù)的圖像和性質(zhì)(2)教案