《廣西柳州市2022年中考數(shù)學(xué) 專題訓(xùn)練04 與圓有關(guān)的計算和證明》由會員分享，可在線閱讀，更多相關(guān)《廣西柳州市2022年中考數(shù)學(xué) 專題訓(xùn)練04 與圓有關(guān)的計算和證明（11頁珍藏版）》請在裝配圖網(wǎng)上搜索。

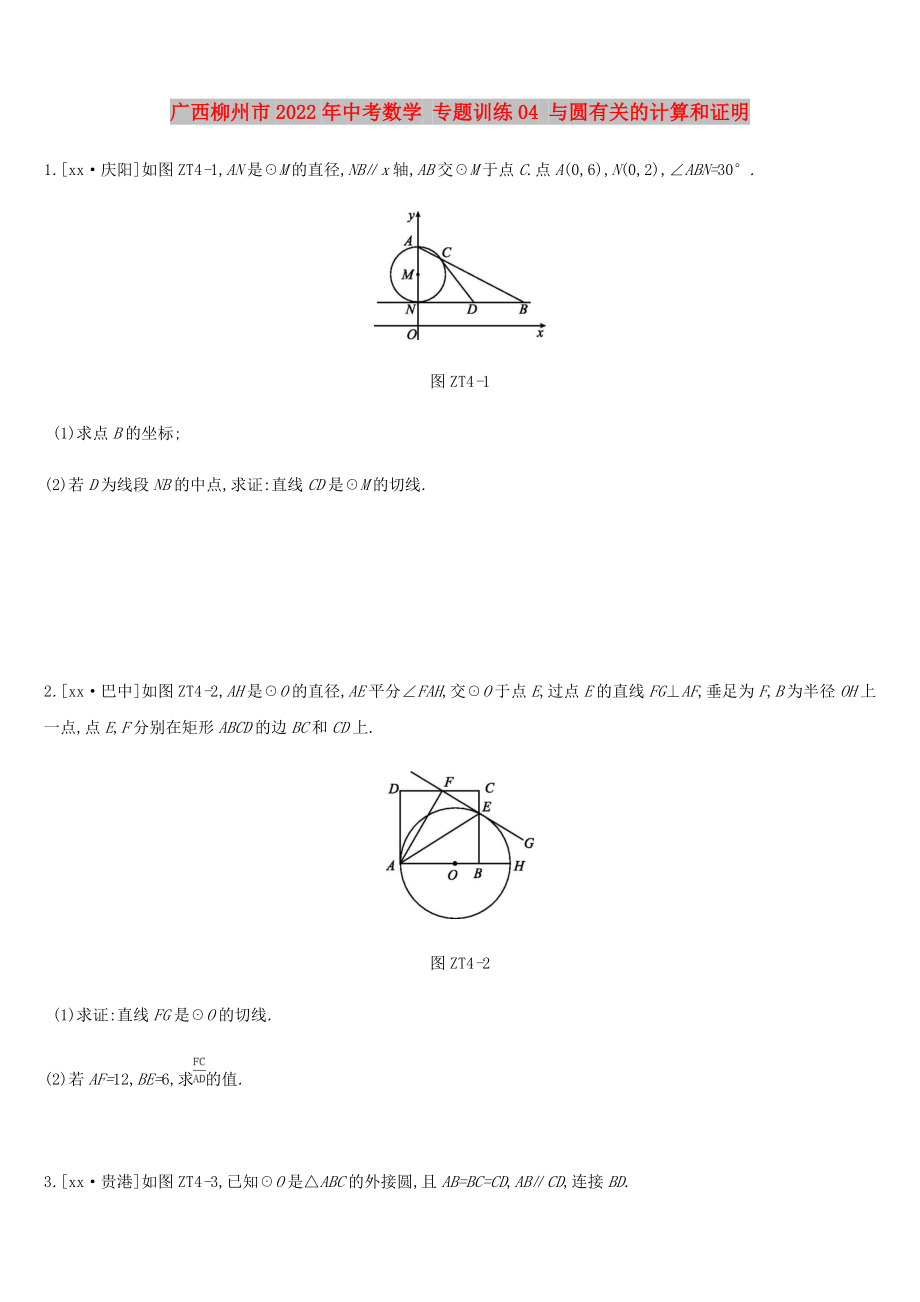
1、廣西柳州市2022年中考數(shù)學(xué) 專題訓(xùn)練04 與圓有關(guān)的計算和證明 1.[xx·慶陽]如圖ZT4-1,AN是☉M的直徑,NB∥x軸,AB交☉M于點C.點A(0,6),N(0,2),∠ABN=30°. 圖ZT4-1 (1)求點B的坐標(biāo); (2)若D為線段NB的中點,求證:直線CD是☉M的切線. 2.[xx·巴中]如圖ZT4-2,AH是☉O的直徑,AE平分∠FAH,交☉O于點E,過點E的直線FG⊥AF,垂足為F,B為半徑OH上一點,點E,F分別在矩形ABCD的邊BC和CD上. 圖ZT4-2 (1)求證:直線FG是☉O的切線. (2)若AF=12,BE=6,求的

2、值. 3.[xx·貴港]如圖ZT4-3,已知☉O是△ABC的外接圓,且AB=BC=CD,AB∥CD,連接BD. 圖ZT4-3 (1)求證:BD是☉O的切線; (2)若AB=10,cos∠BAC=,求BD的長及☉O的半徑. 4.[xx·曲靖]如圖ZT4-4,AB為☉O的直徑,點C為☉O上一點,將沿直線BC翻折,使的中點D恰好與圓心O重合,連接OC,CD,BD,過點C的切線與線段BA的延長線交于點P,連接AD,在PB的另一側(cè)作∠MPB=∠ADC. 圖ZT4-4 (1)判斷PM與☉O的位置關(guān)系,并說明理由; (2)若PC=,求四邊形OCDB的面積.

3、 5.[xx·內(nèi)江]如圖ZT4-5,在☉O中,直徑CD垂直于不過圓心O的弦AB,垂足為點N,連接AC,點E在AB上,且AE=CE. (1)求證:AC2=AE·AB; (2)過點B作☉O的切線交EC的延長線于點P,試判斷PB與PE是否相等,并說明理由; (3)設(shè)☉O的半徑為4,點N為OC中點,點Q在☉O上,求線段PQ的最小值. 圖ZT4-5 6.[xx·廣東]如圖ZT4-6,四邊形ABCD中,AB=AD=CD,以AB為直徑的☉O經(jīng)過點C,連接AC,OD交于點E. 圖ZT4-6 (1)證明:OD∥BC; (2)若tan∠ABC=2,證明:DA與☉O相切;

4、 (3)在(2)的條件下,連接BD交☉O于點F,連接EF,若BC=1,求EF的長. 參考答案 1.解:(1)∵A的坐標(biāo)為(0,6),N(0,2), ∴AN=4. ∵∠ABN=30°,∠ANB=90°, ∴AB=2AN=8, ∴由勾股定理可知NB=4, ∴B(4,2). (2)證明:連接MC,NC.∵AN是☉M的直徑, ∴∠ACN=90°,∴∠NCB=90°. 在Rt△NCB中,D為NB的中點, ∴CD=NB=ND,∴∠CND=∠NCD, ∵MC=MN,∴∠MCN=∠MNC. ∵∠MNC+∠CND=90°, ∴∠MCN+∠NCD=90°,

5、即MC⊥CD. ∴直線CD是☉M的切線. 2.解:(1)證明:連接OE. ∵OA=OE,∴∠OAE=∠OEA. ∵AE平分∠FAH,∴∠HAE=∠EAF, ∴∠FAE=∠OEA, ∴OE∥AF,∴∠OEG=∠AFG. 又∵AF⊥FG,∴∠AFG=90°, ∴∠OEG=∠AFG=90°, ∴OE⊥FG,∴直線FG是☉O的切線. (2)∵四邊形ABCD為矩形, ∴BE⊥AB. ∵EF⊥AF,又∵AE平分∠FAB, ∴EF=BE=6. 又∵四邊形ABCD為矩形, ∴∠D=∠C=90°. ∵∠D=90°,∴∠DAF+∠AFD=90°. 又∵AF⊥FG, ∴∠AF

6、G=90°, ∴∠AFD+∠CFE=90°, ∴∠DAF=∠CFE. 又∵∠D=∠C,∴△ADF∽△FCE, ∴FC∶AD=EF∶AF. ∴FC∶AD=6∶12=1∶2. 3.解:(1)連接BO并延長交AC于H, 由于☉O是△ABC的外接圓,AB=BC,則BH⊥AC且AH=CH, 又∵AB=CD,AB∥CD, ∴四邊形ABDC是平行四邊形,∴AC∥BD, ∴BH⊥BD,即OB⊥BD, ∴BD是☉O的切線. (2)由(1)知,BD=AC, 而AC=2AH=2AB·cos∠BAC=2×10×=12. ∴BD=12. 設(shè)圓的半徑為r,OH=x, 則有r+x=BH,

7、連接AO,在Rt△OAH中,AH2+x2=r2, 又BH===8, ∴r+x=8①. 又由AH2+x2=r2得,(r+x)(r-x)=AH2=36, ∴r-x=②. ①,②聯(lián)立,解得r=, ∴☉O的半徑為. 4.解:(1)過點O作OH⊥PM,連接OD交BC于點E,由于點D為中點,且沿BC折疊與O重合,所以O(shè)D垂直平分BC,OE=OD=OB, 所以∠OBC=30°,所以∠ADC=∠MPB=30°, 則∠POH=60°, 又因為∠POC=2∠OBC=60°, 所以∠POH=∠POC, 又因為∠PHO=∠PCO,PO=PO,所以△PHO≌△PCO, 所以O(shè)H=OC,直線PM

8、到圓心的距離等于半徑,且OH⊥PM,因此PM是☉O的切線. (2)由于D是中點,且沿BC折疊與點O重合, 所以O(shè)B=DB,OC=CD, 又因為OC=OB, 所以O(shè)C=CD=DB=BO, 所以△COD是等邊三角形,四邊形OCDB是菱形,由(1)得出∠CPO=∠HPO=30°, 所以O(shè)C=PC×tan30°=×=1, 則四邊形OCDB的面積為2××1×1×=, 因此四邊形OCDB的面積為. 5.解:(1)證明:如圖,連接BC,∵CD⊥AB, ∴=,∴∠CAB=∠CBA. 又∵AE=CE,∴∠CAE=∠ACE. ∴∠ACE=∠ABC. ∵∠CAE=∠BAC,∴△CAE∽

9、△BAC. ∴=,即AC2=AE·AB. (2)PB=PE.理由如下:如圖,連接BD,OB. ∵CD是直徑,∴∠CBD=90°. ∵BP是☉O的切線, ∴∠OBP=90°. ∴∠BCD+∠D=∠PBC+∠OBC=90°. ∵OB=OC,∴∠OBC=∠OCB. ∴∠PBC=∠D. ∵∠A=∠D,∴∠PBC=∠A. ∵∠ACE=∠ABC,∠PEB=∠A+∠ACE,∠PBN=∠PBC+∠ABC, ∴∠PEB=∠PBN.∴PE=PB. (3)如圖,連接PO交☉O于點Q, 則此時線段PQ有最小值. ∵N是OC的中點,∴ON=2. ∵OB=4,∴∠OBN=30°, ∴∠

10、PBE=60°. ∵PE=PB,∴△PEB是等邊三角形. ∴∠PEB=60°,PB=BE. 在Rt△BON中,BN===2. 在Rt△CEN中,EN===. ∴BE=BN+EN=. ∴PB=BE=. ∴PQ=PO-OQ=-OQ=-4=-4. 6.[解析] (1)連接OC,由SSS可證得△OAD≌△OCD,得∠ADO=∠CDO,由AD=CD可證DE⊥AC,再由AB為直徑證得BC⊥AC,從而得OD∥BC;(2)根據(jù)tan∠ABC=2,可設(shè)BC=a,則AC=2a,AD=AB==a,由OE為中位線知OE=a,AE=CE=AC=a,進一步求得DE==2a,在△AOD中利用勾股定理的逆定理

11、證∠OAD=90°即可;(3)先證△AFD∽△BAD,得DF·BD=AD2,再證△AED∽△OAD,得OD·DE=AD2,從而可得DF·BD=OD·DE,即=,結(jié)合∠EDF=∠BDO知△EDF∽△BDO,據(jù)此可得=,結(jié)合(2)所得相關(guān)線段的長,代入計算可得. 解:(1)證明:連接OC, 在△OAD和△OCD中, ∵ ∴△OAD≌△OCD(SSS), ∴∠ADO=∠CDO. ∵AD=CD, ∴DE⊥AC, ∴∠AEO=90°. ∵AB為☉O的直徑, ∴∠ACB=90°, ∴∠AEO=∠ACB, ∴OD∥BC. (2)證明:∵tan∠ABC==2, ∴設(shè)BC=a,則

12、AC=2a, ∴AD=AB==a. ∵OE∥BC,且AO=BO, ∴OE=BC=a,AE=CE=AC=a. 在△AED中,DE==2a. 在△AOD中,AO2+AD2=a2+(a)2=a2,OD2=(OE+DE)2=a+2a2=a2, ∴AO2+AD2=OD2, ∴∠OAD=90°, 則DA與☉O相切. (3)連接AF, ∵AB是☉O的直徑, ∴∠AFD=∠BAD=90°, 又∵∠ADF=∠BDA, ∴△AFD∽△BAD, ∴=,即DF·BD=AD2. ① ∵∠AED=∠OAD=90°,∠ADE=∠ODA, ∴△AED∽△OAD, ∴=,即OD·DE=AD2. ② 由①②可得DF·BD=OD·DE,即=, 又∵∠EDF=∠BDO, ∴△EDF∽△BDO, ∵BC=1, ∴AB=AD=,OD=,ED=2,BD=,OB=, ∴=,即=, 解得EF=.