《山東省2019年中考數(shù)學(xué) 題型專題復(fù)習(xí) 題型2 圓的證明與計算課件.ppt》由會員分享�,可在線閱讀,更多相關(guān)《山東省2019年中考數(shù)學(xué) 題型專題復(fù)習(xí) 題型2 圓的證明與計算課件.ppt(17頁珍藏版)》請?jiān)谘b配圖網(wǎng)上搜索。
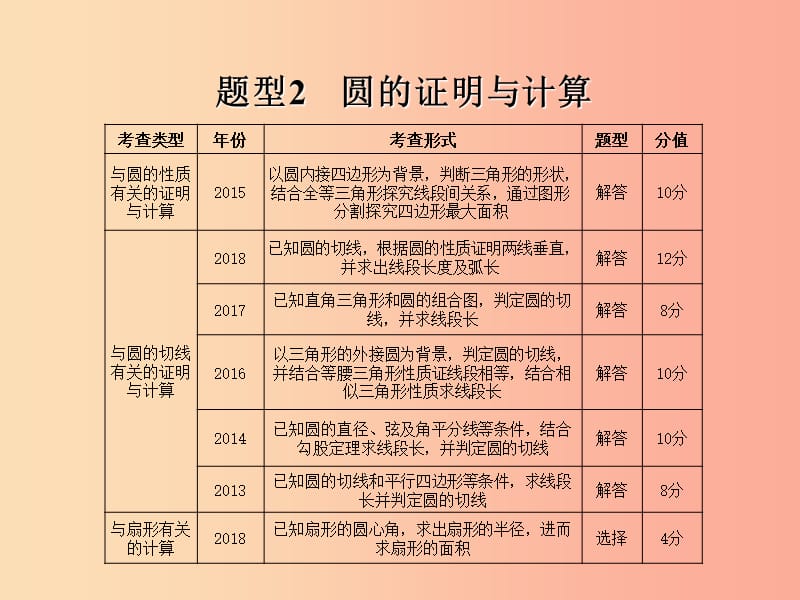
1����、題型2圓的證明與計算,類型與圓的性質(zhì)有關(guān)的證明與計算,例1 2018深圳如圖,在O中���,BC2���,ABAC,點(diǎn)D為 上的動點(diǎn)�����,且cosB . (1)求AB的長度���; (2)求ADAE的值���; (3)過點(diǎn)A作AHBD于H, 求證:BHCDDH.,規(guī)范解答:(1)如圖�����,作AMBC于點(diǎn)M. ABAC�����,AMBC����,BC2, BMCM BC1. 在RtAMB中���,cosABC ����,BM1�����, AB .(5分),(2)如圖����,連接DC. ABAC,ACBABC. 四邊形ABCD內(nèi)接于O���, ADCABC180. ACEACB180����,ADCACE. 又CAE為公共角,EACCAD. �, ADAEAC2( )210
2、.(10分),(3) 證明:如圖�,在BD上取一點(diǎn)N,使得BNCD. 在ABN和ACD中�, ABN ACD(SAS)ANAD. 又AHBD,NHDH. 又BNCD����,BHBNNHCDDH.(15分),滿分技法圓的性質(zhì)綜合運(yùn)用題中,經(jīng)常用到的重要性質(zhì)及技法:運(yùn)用圓是軸對稱圖形也是中心對稱圖形可以對相關(guān)結(jié)論作合理的猜測���;利用垂徑定理�����,通過在由半弦�����、半徑����、弦心距組成的直角三角形����,運(yùn)用勾股定理或銳角三角函數(shù)進(jìn)行計算;在同圓或等圓中�,圓心角、弧����、弦、弦心距等量對等量關(guān)系�����,可以轉(zhuǎn)化相等關(guān)系����;由直徑所對的圓周角是直角構(gòu)造直角三角形;相似三角形���、銳角三角函數(shù)�����、勾股定理是計算線段長度及其線段數(shù)量關(guān)系的重要手段,【
3�����、滿分必練】,C,D,42018宜昌如圖���,在ABC中�����,ABAC���, 以AB為直徑的圓交AC于點(diǎn)D,交BC于點(diǎn)E���, 延長AE至點(diǎn)F����,使EFAE�����,連接FB���,F(xiàn)C. (1)求證:四邊形ABFC是菱形����; (2)若AD7,BE2�����,求半圓和菱形ABFC的 面積,解:(1)證明:AB是直徑�, AEB90���, AEBC. ABAC�, BECE. AEEF���, 四邊形ABFC是平行四邊形 ACAB�����, 四邊形ABFC是菱形,(2)設(shè)CDx.連接BD�����,如圖 AB是直徑���, ADBBDC90, AB2AD2CB2CD2�����, 即(7x)27242x2, 解得x1或8(舍去) AC8����,BD S菱形ABFCACBD8 . S半圓
4、 428.,解:如圖�����,延長AD����,BC交于點(diǎn)E.,52018無錫如圖,四邊形ABCD內(nèi)接于圓O�����,AB17�����,CD10�����,A90,cosB �����,求AD的長,A90�,ADCB180, DCB90.DCE180DCB 90.EEDC90. 又EB90���,BEDC. 在RtECD中,cosBcosEDC . DE CD ����, 在RtECD中,cosB ����, BE AB . EA ADEADE,類型與圓的位置關(guān)系有關(guān)的證明與計算,例22018黃岡如圖,AD是O的直徑�����,AB為O的弦�����,OPAD,OP與AB的延長線交于點(diǎn)P�,過點(diǎn)B的切線交OP于點(diǎn)C. (1)求證:CBPADB; (2)若OA2���,AB1���,求線段BP
5、的長,規(guī)范解答:(1)證明:如圖�����,連接OB. BC是O的切線 OBBC����, OBC90,即OBDDBC90. AD為O的直徑����, ABD90, DBP90����,即CBPDBC90, OBDCBP. OBOD, OBDADB�, CBPADB.(5分),(2)OPAD,POA90�, PA90,PD�, AOPABD, �,即 , BP7.(8分),滿分技法與切線有關(guān)的證明與計算�,最常用的輔助線是連接經(jīng)過切點(diǎn)的半徑,利用直徑構(gòu)造直角三角形�,利用圓周角相等轉(zhuǎn)移角的位置等運(yùn)用三角形全等、三角形相似�����、勾股定理�����、銳角三角函數(shù)等知識進(jìn)行證明與計算,【滿分必練】,A,D,82018湖州如圖�����,已知ABC的內(nèi)切圓O 與
6�����、BC邊相切于點(diǎn)D���,連接OB���,OD.若ABC 40,則BOD的度數(shù)是____,70,92018荊門如圖�,AB為O的直徑,C為O上一點(diǎn)�����,經(jīng)過點(diǎn)C的切線交AB的延長線于點(diǎn)E�,ADEC交EC的延長線于點(diǎn)D,AD交O于點(diǎn)F�����,F(xiàn)MAB于點(diǎn)H���,分別交O����、AC于點(diǎn)M,N�����,連接MB�,BC. (1)求證:AC平分DAE; (2)若cosM �����,BE1�����,求O的半徑�;求FN的長.,直線DE與O相切于點(diǎn)C, OCDE. 又ADDE�����, OCAD.13. OAOC�, 23.12. AC平分DAE.,解:(1)證明:連接OC����,如圖,連接BF,如圖,(2)AB為直徑,AFB90. DEAD���,BFDE.OCBF. �����,COEFA
7����、B. FABM�,COEM. 設(shè)O的半徑為r. 在RtOCE中,cosCOE ���, 即 ����,解得r4�����,即O的半徑為4.,在RtAFB中���,cosFAB �����,AF8 . 在RtOCE中����,OE5,OC4�����,CE3. ABFM���, ����,54. FBDE�����,5E4. 又12����, AFNAEC. ���,即 . FN .,類型與扇形面積有關(guān)的證明與計算,例32018河南如圖�,在ABC中,ACB 90�����,ACBC2�,將ABC繞AC的中點(diǎn) D逆時針旋轉(zhuǎn)90得到ABC,其中點(diǎn)B的運(yùn) 動路徑為 ����,則圖中陰影部分的面積為 _________.,滿分技法求與圓有關(guān)的陰影部分的面積時,常常是通過把不規(guī)則圖形的面積�,用扇形的面積和三角形的面積的和差來解決特別地,對于旋轉(zhuǎn)圖形�,要利用旋轉(zhuǎn)的性質(zhì),確定旋轉(zhuǎn)的中心(扇形的圓心)和旋轉(zhuǎn)半徑(相應(yīng)的線段)的位置的變化�,常常運(yùn)用三角形全等進(jìn)行面積的割補(bǔ),【滿分必練】,A,A,4,D,解:DE與O相切,理由:如圖,連接OD.,OBOD. ODBOBD. BD平分ABC����, EBDOBD, ODBEBD����, ODBE����, ODEE180. DEBC���,E90����, ODE 90����, DEOD, DE與O相切,142018泰州如圖���,AB為O的直徑�,C為O上一點(diǎn)�����,ABC的平分線交O于點(diǎn)D�����,DEBC于點(diǎn)E. (1)試判斷DE與O的位置關(guān)系,并說明理由,
 山東省2019年中考數(shù)學(xué) 題型專題復(fù)習(xí) 題型2 圓的證明與計算課件.ppt
山東省2019年中考數(shù)學(xué) 題型專題復(fù)習(xí) 題型2 圓的證明與計算課件.ppt